【量子計算機の優位性】量子超越性と暗号の安全性は等価らしい
日本の研究グループが量子超越性と暗号の安全性が等価であることを証明したというニュースを目にしました。
難しいのでNotebookLMに解説してもらいながら概要だけでも確認してみます。
世界初、量子超越性と暗号の安全性が等価であることを証明
2025年6月23日、NTTのWebサイトに掲載されたニュースリリースにて、基礎物理学研究所(京都大学)とNTT社会情報研究所の研究グループによる研究成果として、量子計算機が古典計算機よりも高速であることの必要十分条件を暗号理論の観点から明らかにしたという公表がありました。
研究で示されたこと
- 量子超越性と暗号の安全性が等価であること
- 量子超越性が存在しない場合、現在安全とされている暗号機能の多くが破られること
計算の種類によっては、量子計算機(量子コンピュータ)の計算能力が古典的な計算機のそれに比べて高いということ(量子超越性)はなんとなく理解、信用していましたが、それを確認するための基準(必要十分条件)というものは実は明確ではなかったそうです。今回の研究で、その条件が暗号理論との関係性によって説明されています。
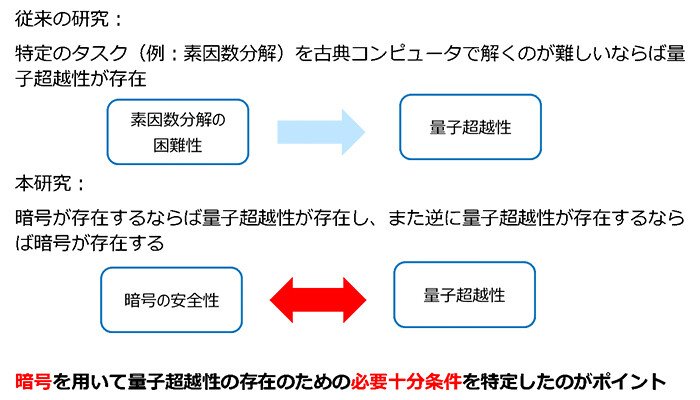
また、「もし量子超越性が存在しないのであれば、現在安全とされている多くの暗号機能の安全性が破綻してしまう」ことも示されており、これは情報セキュリティ分野との関連性も深い内容です。ここで安全性が破綻すると指摘されている暗号機能は量子暗号だけではなく、従来の古典計算機上の暗号(量子計算機によって破られてしまうとされる暗号)や今後の普及が急がれている耐量子計算機暗号(PQC)も含みます。

論文は以下から。お詳しい方は原文をどうぞ。
(参考)NISTによるPQCの標準化
PQCの話も出たので、参考までにNIST(米国立標準技術研究所)によるPQCの標準化の状況にも触れておきます。
2024年8月、3つのPQCの方式がNISTにより標準化されました。現在も他の方式の検討が進められています。
このプロジェクトでは、CRQC(Cryptographically Relevant Quantum Computer、従来のコンピュータでは実行不可能な実際の暗号システムに対する攻撃が可能な量子コンピュータ)を想定してPQCの標準化が進められています。つまり、前述の量子超越性のような理論的な枠組みというよりは、実際に暗号が破ることができる能力を有する量子コンピュータが現れることを想定した取り組みであると解釈できます。主旨は異なるものの、土台となる量子や暗号といった技術要素は共通です。
The goal of post-quantum cryptography (also called quantum-resistant cryptography) is to develop cryptographic systems that are secure against both quantum and classical computers, and can interoperate with existing communications protocols and networks.
出典:Post-Quantum Cryptography | CSRC
Q: What is a quantum computer, and how is it different from the computers we use today?
A: Quantum computers can, in principle, perform certain mathematical algorithms exponentially faster than a
classical computer. In place of ordinary bits used by today’s computers, quantum computers use “qubits” that
behave and interact according to the laws of quantum mechanics. This quantum physics-based behavior would enable a sufficiently large-scale quantum computer to perform specific mathematical calculations that would be infeasible for any conventional computer.Q: What is a “Cryptographically Relevant Quantum Computer” (CRQC)?
A: Small, laboratory-scale examples of quantum computers have been built. Some larger systems have also
been proposed that can address some types of computation, but which may not be suitable for analyzing
cryptographic algorithms. CRQC is used to specifically describe quantum computers that are capable of actually attacking real world cryptographic systems that would be infeasible to attack with a normal computer.出典:NISTのFAQ
Q: What is the threat if a CRQC were developed?
A: If realizable, a CRQC would be capable of undermining the widely deployed public key algorithms used for asymmetric key exchanges and digital signatures. National Security Systems (NSS) — systems that carry classified or otherwise sensitive military or intelligence information — use public key cryptography as a critical component to protect the confidentiality, integrity, and authenticity of national security information. Without effective mitigation, the impact of adversarial use of a quantum computer could be devastating to NSS and our nation, especially in cases where such information needs to be protected for many decades.
キーワードや定理
論文からいくつか引用します。
- 非効率検証可能量子性証明(IV-PoQ: Inefficient-Verifier Proofs of Quantumness)
- 一方向性パズル(OWPuzzs: One-Way Puzzles)
- 対話型量子優位性サンプラー(Int-QASs: Interactive Quantum Advantage Samplers)
- QAS/OWF条件(QAS/OWF Condition)
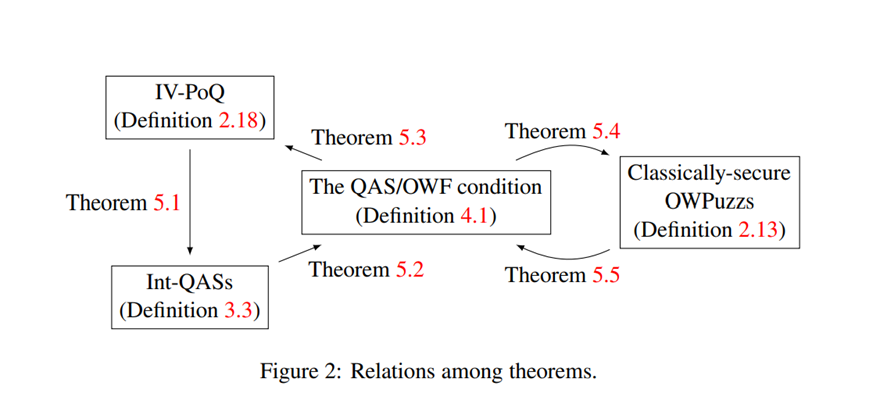
- IV-PoQが存在するならば、Int-QASsが存在する (Theorem 5.1)
- Int-QASsが存在するならば、QAS/OWF条件が満たされる (Theorem 5.2)
- QAS/OWF条件が満たされるならば、IV-PoQが存在する (Theorem 5.3)
- QAS/OWF条件が満たされるならば、古典的に安全なOWPuzzsが存在する (Theorem 5.4)
- 古典的に安全なOWPuzzsが存在するならば、QAS/OWF条件が満たされる (Theorem 5.5)
と、
- 非効率検証可能量子性証明 (IV-PoQ) が存在することと、古典的に安全な一方向性パズル (OWPuzzs) が存在することが必要十分である (Theorem 1.1)
Theorem 1.1. Inefficient-verifier proofs of quantumness (IV-PoQ) exist if and only if classically-secure
出典:Cryptographic Characterization of Quantum Advantage
one-way puzzles (OWPuzzs) exist.
5 Equivalence of IV-PoQ and Classically-Secure OWPuzzs
出典:Cryptographic Characterization of Quantum Advantage
Our main result, Theorem 1.1, that IV-PoQ exist if and only if classically-secure OWPuzzs exist is obtained
by combining the following theorems. (For relations among these theorems, see Figure 2.)
Theorem 5.1. If IV-PoQ exist, then Int-QASs exist.
Theorem 5.2. If Int-QASs exist, then the QAS/OWF condition is satisfied.
Theorem 5.3. If the QAS/OWF condition is satisfied, then IV-PoQ exist.
Theorem 5.4. If the QAS/OWF condition is satisfied, then classically-secure OWPuzzs exist.
Theorem 5.5. If classically-secure OWPuzzs exist, then the QAS/OWF condition is satisfied.
内容が知りたくなってきた方は、論文か、以降のNotebookLMによる解説をご覧ください。
NotebookLMによる解説
NotebookLMに、この論文について解説してもらいました。
特に、IV-PoQ、Int-QASs、QAS/OWF条件、OWPuzzsの意味のつながりを順を追って説明し、専門用語は補足や言い換えで解説するよう指示しています。数式は含まない解説です。
IV-PoQ、Int-QASs、QAS/OWF条件、OWPuzzsの意味のつながり
この研究は、量子計算機が古典計算機よりも優位性を持つとされる「量子超越性」がどのような条件の下で存在するのか、という根本的な問いに対し、暗号理論の観点から初めて明確な必要十分条件を与えた画期的な成果です。
具体的には、「非効率検証可能量子性証明(IV-PoQ)」が存在することと、「古典的に安全な一方向性パズル(OWPuzzs)」が存在することが論理的に等価であることを証明しました。
以下に、関連する専門用語を補足しながら、これらの概念がどのように繋がっているのかを順を追って説明します。
1. 量子超越性(Quantum Computational Advantage)とは?
「量子超越性」とは、ある特定の計算課題において、量子計算機が古典計算機よりも真に高速であることを指します。例えば、古典計算機では途方もない時間がかかる問題でも、量子計算機なら短時間で解ける、というような優位性のことです。 この量子超越性が「無条件で存在する」(つまり、どんな場合でも存在する)ことを示すのは、現在の複雑性理論(計算の難しさを研究する分野)の理解を超えており、非常に困難です。そのため、これまでは「もしある問題がこれくらい難しければ、量子超越性が存在する」といった形で、何らかの「計算上の仮定」(前提条件)のもとでその存在が示されてきました。しかし、それらの仮定が本当に「必要」なのかは、これまで不明だったのです。
2. 非効率検証可能量子性証明(IV-PoQ: Inefficient-Verifier Proofs of Quantumness)とは?
IV-PoQは、量子超越性を特徴づけるためにこの研究で中心的に扱われる概念です。これは一種の**「量子計算能力の証明書」のような対話型プロトコル**だと考えると分かりやすいでしょう。
- 登場人物:
- 証明者(Prover: P): 量子計算機を持つ側(量子多項式時間アルゴリズム、QPT)。
- 検証者(Verifier: V): 古典計算機しか持たない側。Vは、効率的な部分(V1、古典多項式時間アルゴリズム、PPT)と、非効率的だが最終的な判定に無制限の時間を使える部分(V2、無制限アルゴリズム)に分かれています。
- プロトコルの流れ:
- 第1フェーズ: 証明者Pと効率的検証者V1が、古典的な通信チャネルを通じてメッセージをやり取りします。このやり取りの全てが記録され、「トランスクリプト」と呼ばれる一連の古典的なメッセージ列が生成されます。
- 第2フェーズ: 無制限の計算能力を持つ検証者V2が、第1フェーズで得られたトランスクリプトを受け取ります。V2は、このトランスクリプトが本当に量子計算能力を持つ証明者によって生成されたものなのかどうかを検証し、最終的な判断(「受理」または「棄却」)を下します。
- IV-PoQの「健全性(Soundness)」:
- もし証明者Pが本物の量子計算機(QPT)であれば、検証者V2は高い確率で「受理」します(これを「完全性」と呼びます)。
- しかし、もし**偽の証明者P*が古典計算機(PPT)**であった場合、検証者V2は高い確率で「棄却」します(これを「健全性」と呼びます)。
- この「健全性」の条件が、「古典計算機では不可能な計算を量子計算機は行える」という量子超越性の本質を捉えているわけです。
- IV-PoQは、サンプリング問題ベースの量子超越性(ある確率分布からのサンプル生成)や、探索問題ベースの量子超越性(ある問題の解を見つける)など、これまで研究されてきた様々なタイプの量子超越性を包括できるとされています。
3. 一方向性パズル(OWPuzzs: One-Way Puzzles)とは?
一方向性パズルは、量子暗号の分野で提唱された基本的な暗号の構成要素です。
- 構成要素:
- パズル作成アルゴリズム(Samp): 量子多項式時間(QPT)アルゴリズムであり、実行すると「パズル(puzz)」とそれに対応する「解答(ans)」のペアを出力します。
- パズル検証アルゴリズム(Ver): 無制限の計算能力を持つアルゴリズムであり、パズルと任意の解答候補を受け取り、その解答が正しいかどうかを判定します。
- 重要な性質:
- 正当性(Correctness): Sampが生成したパズルと解答のペアは、Verによって常に正しいと判定されます。
- 安全性(Security): 生成された「パズル」だけが与えられた場合、古典的な多項式時間アルゴリズム(PPT、つまり古典計算機)では、対応する「解答」を高い確率で見つけることができません。
- この研究では特に**「古典的に安全なOWPuzzs」**に焦点を当てています。これは、量子計算機はパズルを解くことができるかもしれないが、古典計算機には解けない(つまり、古典的な攻撃者に対して安全である)という意味です。
- OWPuzzsは、古典暗号の基礎となる「一方向性関数(OWF)」よりも弱い仮定で存在し得ると考えられており、**擬似乱数ユニタリー(PRUs)や擬似乱数状態生成器(PRSGs)**など、多くの量子暗号プリミティブが存在するならば、OWPuzzsも存在することが示されています。
- これまで、OWPuzzsの応用例は「コミットメント(約束手形のような暗号機能)」に限定されていましたが、本研究によって「量子超越性」が新たな応用例として加わりました。しかも、これは量子計算と古典通信(QCCC)を組み合わせた応用としては初めてのものです。
4. 対話型量子優位性サンプラー(Int-QASs: Interactive Quantum Advantage Samplers)とは?
これは、この研究で新しく導入された概念で、IV-PoQとOWPuzzsを結びつけるための重要な中間ステップです。
- **量子優位性サンプラー(QAS: Quantum Advantage Samplers)**という概念の拡張版です。QASとは、「ある確率分布を量子計算機なら効率的にサンプリングできるが、古典計算機にはそれが難しい」という性質を持つサンプラーを指します。これは、サンプリングベースの量子超越性の「平均ケース版」と見なすことができます。
- Int-QASsは、このQASを「対話型」に一般化したものです。具体的には、2つの量子多項式時間アルゴリズム(AとC)が対話して生成する通信記録(トランスクリプト)の確率分布を、古典的な多項式時間アルゴリズムが効率的に模倣できない、という性質を指します。
5. QAS/OWF条件(QAS/OWF Condition)とは?
これもまた、この研究で新しく導入された概念で、IV-PoQとOWPuzzsの間に架け橋をかけます。
- この条件は、直感的には**「量子優位性サンプラー(QAS)が存在するか、または古典的に安全な一方向性関数(OWF)が存在する」**という概念を、より厳密な形で表現したものです。
- 「一方向性関数」とは、計算は簡単だが、その逆を計算するのは非常に難しい関数であり、古典暗号の最も基本的な前提条件です。
- この条件は、OWPuzzsとIV-PoQの間の論理的な等価性を証明するために「枢軸となる役割」を果たします。
各概念のつながり(順を追って説明)
この研究の主要な成果である「IV-PoQの存在 ⇔ 古典的に安全なOWPuzzsの存在」は、以下の定理の連鎖によって証明されました。
- IV-PoQが存在するならば、Int-QASsが存在する (Theorem 5.1)。
- これは直感的にも分かりやすい関係です。もしIV-PoQ(量子計算能力の証明)が存在するのに、その第1フェーズでの量子証明者と古典検証者間の対話記録(トランスクリプト)が、古典的な偽の証明者によって容易に模倣できてしまうとしたら、IV-PoQの「健全性」(古典計算機では量子能力を偽装できないこと)が破綻してしまいます。
- したがって、IV-PoQが存在するならば、その対話記録の生成自体が、古典計算機にとっては難しい、すなわちInt-QASsが存在する、ということになります。
- Int-QASsが存在するならば、QAS/OWF条件が満たされる (Theorem 5.2)。
- この証明は、背理法を用いています。もしQAS/OWF条件が満たされないと仮定すると、それは「量子優位性サンプラーの出力分布を古典的に効率よく近似できてしまう」かつ「古典的に安全な一方向性関数が存在しない」という状況を意味します。
- この状況では、Int-QASsを破る古典的なアルゴリズムを構築できてしまうことが示されます。これはInt-QASsの定義に矛盾するため、最初の仮定(QAS/OWF条件が満たされない)が誤りである、つまりQAS/OWF条件は満たされる、と結論されます。
- QAS/OWF条件が満たされるならば、IV-PoQが存在する (Theorem 5.3)。
- QAS/OWF条件が満たされるということは、大まかに言って「量子優位性サンプラー(QAS)が存在する」か「古典的に安全な一方向性関数(OWF)が存在する」かのどちらかが成り立ちます。
- もしOWFが存在するならば、既存の研究成果によってIV-PoQを構築できることが既に知られていました。
- もしQASが存在するならば、研究者たちはコルモゴロフ複雑性(あるデータを表現するのに必要な最短のプログラムの長さ。データがランダムであるほど長くなる)という概念を利用して、非対話型のIV-PoQを構築できることを示しました。QASの出力は古典的には模倣困難なため、「非常にランダム」であり、そのコルモゴロフ複雑性が高いことを利用するのです。
- これらを組み合わせることで、QAS/OWF条件からIV-PoQを構築できることが証明されます。
- QAS/OWF条件が満たされるならば、古典的に安全なOWPuzzsが存在する (Theorem 5.4)。
- これも上記と同様に、QASかOWFのどちらかが存在する場合に分けて証明されます。
- もしOWFが存在するならば、そのOWFを使って古典的に安全なOWPuzzを比較的簡単に構築できます。OWFの入力をOWPuzzの解答に、OWFの出力をOWPuzzのパズルに対応させれば良いのです。
- もしQASが存在するならば、上記のステップ3でQASから構築した非対話型IV-PoQを応用して、OWPuzzを構築できることが示されます。
- 古典的に安全なOWPuzzsが存在するならば、QAS/OWF条件が満たされる (Theorem 5.5)。
- これも背理法で証明されます。もしQAS/OWF条件が満たされないと仮定すると、それはOWPuzzの「安全性」を破る古典的な攻撃者を構築できてしまうことを意味します。
- これはOWPuzzの定義に矛盾するため、元の仮定(QAS/OWF条件が満たされない)が誤りである、つまりQAS/OWF条件は満たされる、と結論されます。
この一連の連鎖的な証明(IV-PoQ ⇔ Int-QASs ⇔ QAS/OWF条件 ⇔ 古典的に安全なOWPuzzs)によって、最終的に**「量子超越性の存在」と「古典的に安全な一方向性パズルの存在」が数学的に等価である**ことが示されたのです。
本研究の意義と波及効果
- 量子超越性の初の完全な特徴付け: 量子計算機の優位性が、どのような暗号学的仮定(前提)の上に成り立っているのかを初めて明確にしました。
- 既存研究の未解決問題の解決: 以前の研究ではOWF(一方向性関数)からIV-PoQを構築できましたが、より弱い仮定からの構築は未解決でした。本研究はOWFより弱いOWPuzzsからIV-PoQを構築できることを示し、この問題を解決しました。
- 量子暗号の安全性への影響: この研究結果は、「もし量子超越性が存在しないのであれば、現在安全とされている多くの量子暗号プリミティブの安全性が破綻してしまう」という非常に重要な示唆を含んでいます。これには、擬似乱数ユニタリー (PRUs) や 擬似乱数状態生成器 (PRSGs) などが含まれます。これは、情報セキュリティ分野にとって大きな意味を持ち、量子計算の優位性が暗号の基盤と深く結びついていることを示しています。
- OWPuzzsの新たな応用: これまでコミットメント機能にしか応用が知られていなかったOWPuzzsに、量子超越性という新たな応用例を見出した点も重要です。特に、量子計算と古典通信(QCCC)の枠組みにおけるOWPuzzsの初の応用であり、以前からのオープン問題を解決しました。
この研究は、量子計算機の理論的な理解を深めるとともに、将来のセキュアな暗号システム設計に向けた強固な基盤を提供するものです。
総括としてTheorem 1.1. の解説
Theorem 1.1は、Tomoyuki Morimae氏、Yuki Shirakawa氏、Takashi Yamakawa氏による論文「Cryptographic Characterization of Quantum Advantage」の主要な結果であり、「非効率検証可能量子性証明 (IV-PoQ) が存在することと、古典的に安全な一方向性パズル (OWPuzzs) が存在することが必要十分である」と述べています。これは、量子計算優位性 (Quantum computational advantage) の完全な暗号学的特徴付けが初めて得られたことを意味するとされています。
Theorem 1.1の重要性と波及効果は、主に以下の5つの点にまとめられます。
- 量子優位性の初の完全な暗号学的特徴付け: 量子優位性の存在にとって何が必要かつ十分であるかについて、明確な解答を与えました。これは、これまでの研究が十分条件に留まっていた点を大きく改善するものです。
- 既存のオープン問題の解決:
- 以前の研究 [Morimae and Yamakawa, Crypto 2024] では、IV-PoQを一方向性関数 (OWFs) から構築できることが示されていましたが、より弱い仮定からの構築は未解決問題でした。本研究は、OWFsよりも弱いとされるOWPuzzsからIV-PoQを構築できることを示し、この問題を解決しました。
- これまで、コミットメント以外にOWPuzzの応用は知られていませんでした。本結果は、量子優位性がOWPuzzの新たな応用例であることを示しました。
- さらに、IV-PoQが量子計算・古典通信 (QCCC) プリミティブであることから、OWPuzzの初のQCCCアプリケーションとしても位置づけられ、[Chung, Goldin, and Gray, Crypto 2024] のオープン問題も解決しました。
- 量子暗号プリミティブの基盤: OWPuzzは多くの重要な量子暗号プリミティブ(PRUs、PRSGs、OWSGsなど)によって導かれるため、本結果は「もし量子優位性が存在しないならば、これらの量子暗号プリミティブの多くも存在しない」ことを示唆します。
- 情報セキュリティへの示唆: 量子優位性が存在しない場合、現在安全とされている多くの暗号機能(量子暗号だけでなく、広く利用されている古典計算機上の暗号や今後の耐量子計算機暗号も含む)の安全性が破綻する可能性があることを意味しており、情報セキュリティ分野にとっても重要な示唆を与えています。
- 新たな理論的基盤の提供: 量子計算理論と暗号理論という一見関係のない二つの分野を結びつけ、量子優位性の実証実験やさらなる理論研究が、暗号理論に基づいたより強固な基盤の上で進められることが期待されます。
まとめ
量子超越性と暗号の安全性が等価であることを証明した論文の話題でした。
NotebookLMは便利ですね。自力では全く読めないような論文にこうやって多少でも触れることができます。
あと、余談ですが、こういった技術動向の把握に合わせて資産形成の参考になりそうな株価情報をチェックできるようにしておくのも良いですね(今回の発表で特に大きな動きはありませんが)。量子コンピューティング関連銘柄の動向など、注目テーマごとに動向をチェックしたい場合はmoomoo証券が便利かと思います。私はSBI証券をメインにしています。

ポイ活や資産運用に関する記事も投稿しています。もし興味がありましたらどうぞ。

この記事をポッドキャスト風のAI音声で聞き流し
NotebookLM