【スッキリ】鏡に映すと上下でなく左右だけ反転して見えるワケ

私の隣にいた人が、ふと鏡に映ったデジタル時計の”2″という数字を”5″と読み上げました。ゴールデンウィーク最終日のことです。

そういえば昔、”どうして、鏡に映ったものは上下には反転せず、左右だけ反転するのだろう？“、と不思議に思ったこともありましたが、解決できていないままでした。

気になりだしたら頭から離れなくなってしまい、その日は、用事をこなしながら一日中、この鏡の反転問題について考えていました。

ということで、本記事では、”鏡に映すと上下でなく左右だけ反転して見えるワケ”についてまとめます。※長文なのでお時間のある方はどうぞ

なお、専門知識は無いので、記事中では用語を適宜定義しています。
また、説明に使用している図も若干リアリティには欠けますが、ご了承ください。

本記事で説明する答え

本記事では、”鏡の反転問題”の答えを、以下のように説明します。

• 鏡に映すこと自体により左右反転はしないが、鏡の反射は “あっちを向いているものをこっちに見せるはたらき” があるので、結果的に左右反転して見える

これから説明する前提事項や3つの観点から、この答えにたどり着きます。

また、反転の状態を式で計算して求められるよう、定式化(もどき)をします。

さらに理解を深めるため、別解として、左右反転でなく、”上下反転して見えるケースもあり得る” という話も添えます。

前提

用語定義

本記事では、以下の用語を用います。

観測者

見る主体です。
本記事では、”人”を指します。

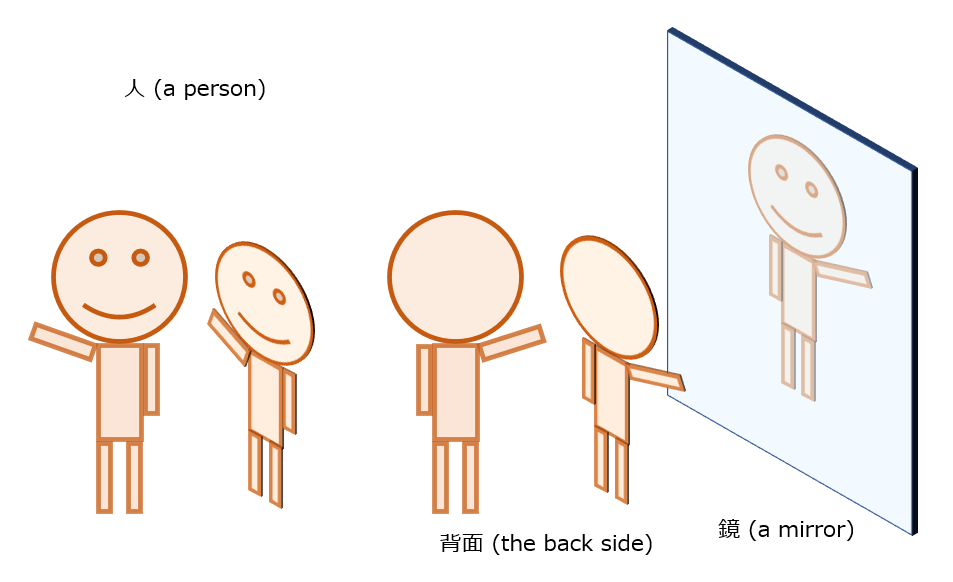
一部、説明のため、”カメラ” のように撮影できるものを “人” の代わりに使う場合があります。

鏡

普通の鏡です。光を反射します。

対象物

見られる対象です。
本記事では、以下のように半透明のカードに文字”R”と書いたもの(のようなもの)を主な対象物として用います。裏から見ると、文字が透けて見えます。

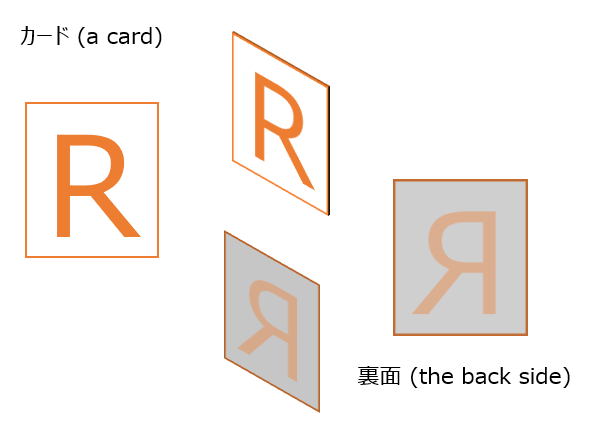
文字カード以外に、観測者が鏡に映った自分を見る場合もあります。観測者自身が対象物を兼ねている状態です。

東西南北と天地

前後左右や上下という方向は、観測者の向きによって相対的に決まります。
それらとは別に、観測者の向きと関係なく絶対的に決まる方向を定義しておきます。

便宜的に、東西南北と天地とします。本記事において、これらは観測者の向きが変わっても一定です。

(全く立体感が無いですが)

視線

観測者の目から対象物(視点)までの線、およびその方向です。
本記事では、単に”線”でなく、方向も含めます。

観測者は、対象物、あるいは、対象物の像(鏡による反射時)を見ます。
そのとき、観測者の目から視点(注視点)に対し、視線が生じるものとします。

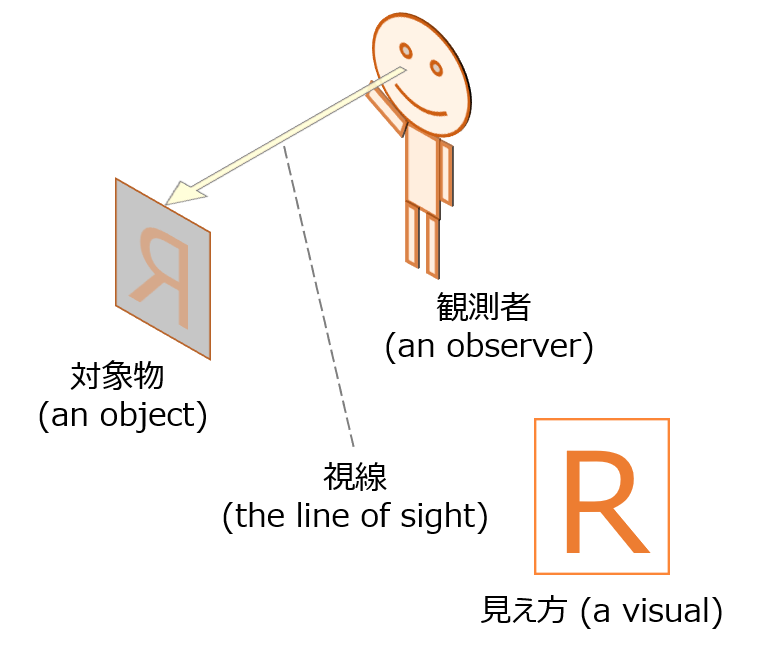
見え方

観測者から、対象物がどのように見えるかということです(上記の”視線”の図を参照)。

反転

本記事で扱う “反転” は、見え方の違いを表したものです。

つまり、見る主体である観測者がいる場合にのみ、”反転” が発生します。

観測者が対象物を見た際、その見え方が、基準となる別の見え方と比較して特定の違いがある場合、その見え方は “反転” していると言えます。

具体的には、以下3つの条件をすべて満たした状態を、”反転”として扱います。

• 1. 観測者(見る主体)がいる
• 2. 観測者の視線で対象物を見た際、その見え方を、基準となる別の見え方と比較できる
• 3. 比較の結果、以下のいずれか、もしくは以下を組み合わせた違いがある
  • 基準となる見え方では右側にあった部分が左側に見えて、逆に左側にあった部分が右側に見える(左右反転)
  • 基準となる見え方では上側にあった部分が下側に見えて、逆に下側にあった部分が上側に見える(上下反転)
  • 基準となる見え方では前(表)側にあった部分が後(裏)側に見えて、逆に後(裏)側にあった部分が前(表)側に見える(前後反転)

左右反転、上下反転、前後反転の3種類を挙げました。
組み合わせて、上下左右反転、等もあります。

※他の要素の反転(色、明暗、等)については、本記事の対象外です。

鏡の反転問題

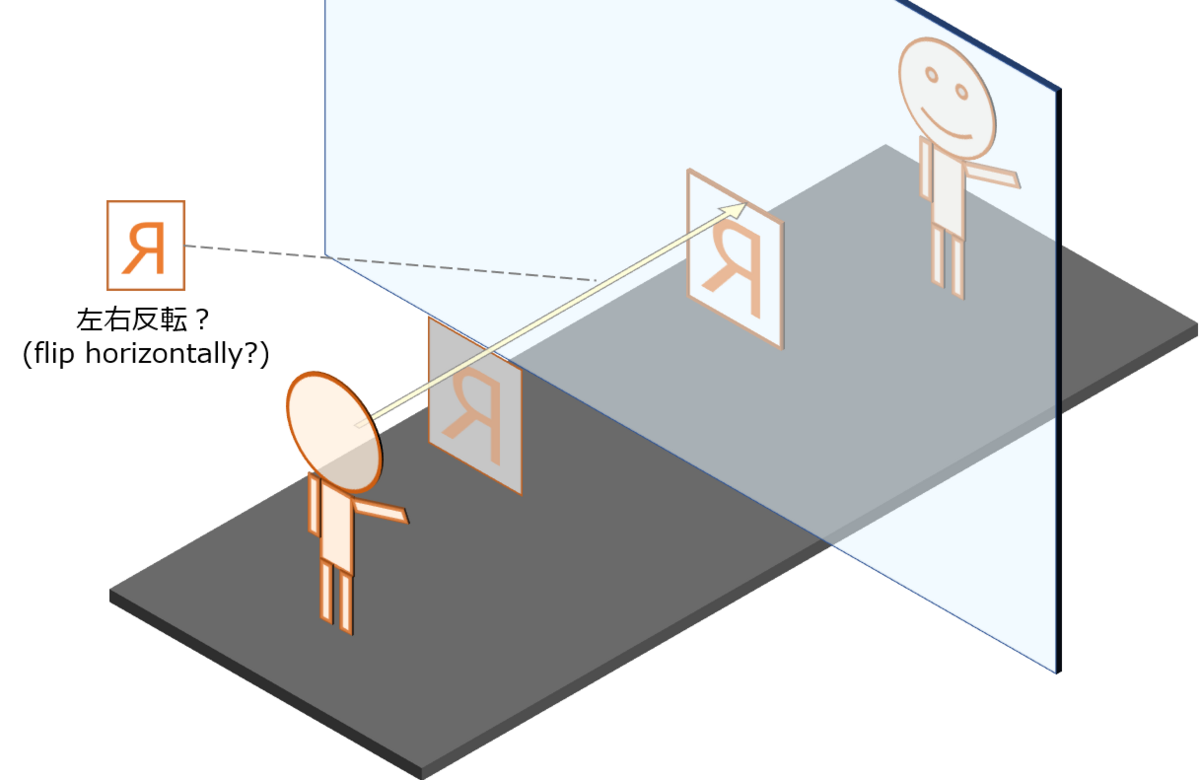
本記事で扱う、”鏡に映った像の見え方が、上下には反転せず、左右だけ反転しているのはなぜか”、という問題です。

反転が発生するケース (パラメタ)

前提事項として、上記の用語を用いて、カードに書かれた文字”R”の反転が発生するケースを3つ挙げます。

これらは、鏡の反転問題を考える上でのパラメタです。

No.	分類	動作	発生する反転
1	対象物の向き	対象物を裏返す	・前後反転 ・裏返す方向に反転(左右、上下)
2	観測者の向き	観測者が対象物の裏に回り込む	・前後反転 ・回り込む方向に反転 　(左右、上下)
3	(光の)反射	鏡に映った像を見る	・鏡面に対して垂直に反転 　(左右、上下、前後)

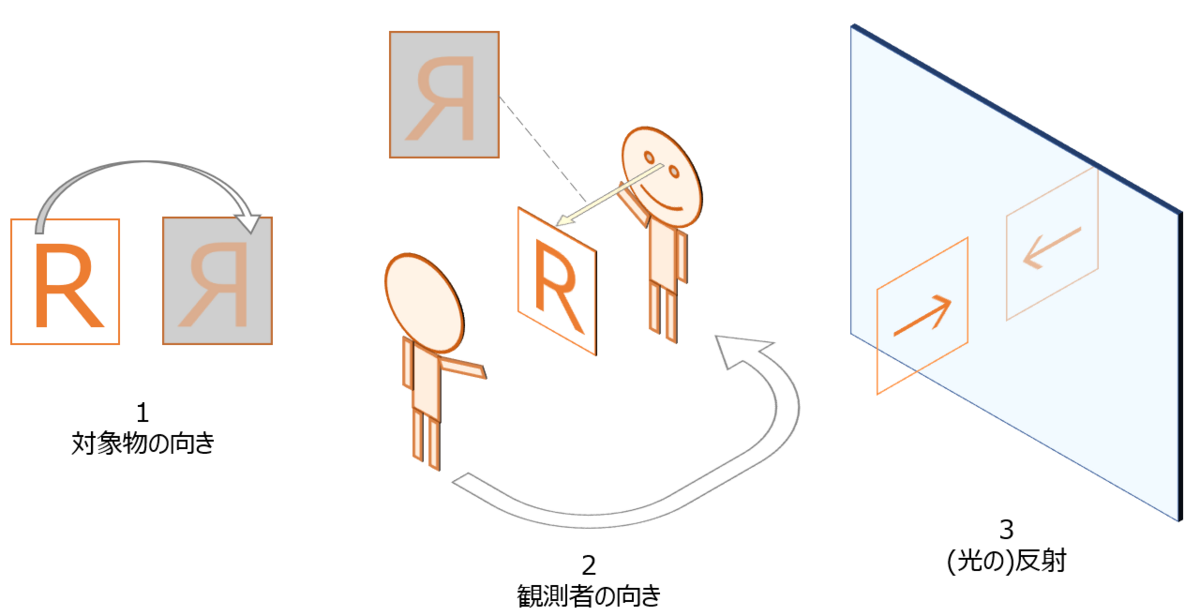
本記事は、鏡の左右反転問題を整理するためのものなので、上記の3つに絞ります。

なお、文字カードを裏から見た場合に、左右反転あるいは上下反転しているかどうかは、裏から透けて見える文字の見え方によって判断します。

この反転が発生するケースについては、以下の補足記事にまとめてあります。

鏡の反転問題を紐解く

前置きが長くなりましたが、いよいよ”鏡の反転問題”を紐解いていきます。

用いる図は以下です。

観測者が、対面する鏡越しに対象物を見ています。

対象物が文字カードの場合と、観測者自身(自分)の場合で、説明を分けた方が分かりやすそうなので、それぞれ説明します(もちろん物理的には説明を分ける必要性はなく、同じ現象です)。

文字カードの反転

文字カードを対象物とした場合についてです。

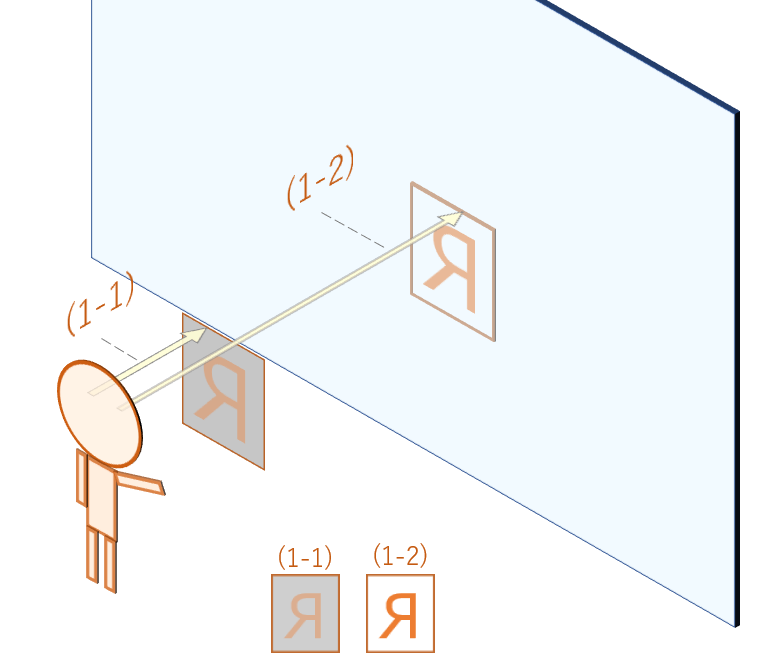
整理のため、観測者の視線とその見え方にそれぞれ番号を割り振ります。

まずは反転している様子を確認

最初に、”どうして、鏡に映ったものは上下には反転せず、左右だけ反転するのだろう？”という疑問の出発点を確認します。

鏡に映った文字カードは、(1-2)です。

(1-2)の見え方は、Rが正しく読めない向きになっています。

確かに左右反転しているように見えます。しかし上下反転はしていないように見えます。

このような見え方になるのはなぜか、というのがこの疑問の出発点です。

疑問を解決するための3つの観点

この疑問を解決するため、以下3つの観点について考えます。

• 観点1 反転しているかどうかを判断するための基準
• 観点2 観測者の向きの違いによる影響
• 観点3 対面する鏡のはたらき

観点1 反転しているかどうかを判断するための基準

まずは、”鏡に映すことで左右反転している”という判断が正しいのか、確認していきます。

定義に照らす

前述の定義に照らすと、左右反転は、”基準となる見え方では右側にあった部分が左側に見えて、逆に左側にあった部分が右側に見える”という状態のことです。

つまり、基準となる見え方との比較に基づいて判断しなければいけません。

そういえば、そもそも何を基準にして “左右反転している” と判断したのかが不明確でした。

鏡に映せないものは基準にできない

観測者の位置からは、文字カードの裏しか見えません。ちなみに、文字カードの裏から透けて見える(1-1)と、鏡に映った(1-2)を比較しても左右反転などしていません。

つまり、”(1-2)が左右反転している”という判断は、実際には観測者の視界に無いものを基準に比較したことになります。

視界に無い基準となると、記憶(知識)を頼ることになります(※1)。観測者の記憶の中にある文字”R”は、もちろん文字として読める”R”でしょうから(※2)、それと比較すれば、(1-2)は左右反転していることになります。
(※1)(※2) 認知という意味で、この2つの仮定が正しいことを説明するのは難しそうです。ただ別の観点から補足すると、どの見え方を基準にした場合も、本記事で説明する反転の仕組み自体は変わらないので、記事の主旨に影響はありません。おそらく最も分かりやすいであろう例として、文字として読める”R”の見え方を基準に話を進めるということです。

しかし、ここで注意が必要です。

記憶の中の”R”は鏡に映せないということです。

つまり、記憶の中の”R”を基準にしたままでは、(1-2)の見え方が “鏡によって反転されたものかどうか” を判断することができません。

基準となる見え方を改めて決める

(1-2)が “鏡によって反転されたかものどうか” を判断するために、基準を決め直します。

そこで、図の中から、記憶の中の “R” (文字として読める”R”) と同じ見え方を探すことにします。

基準を図の中にある見え方に置き換えることで、後述の観点2,3を踏まえて、鏡に映った (1-2) の見え方との “比較” ができるからです。

ちょうど(1-3)の見え方が、文字として読める “R” と同じなので、これを基準にします。

(1-2)と(1-3)を比較すると、確かに左右反転しています。

しかし、(1-3)は観測者の位置からは見えないので、(1-2)が “鏡によって反転されたかものどうか” を判断するためには、他の観点も考慮する必要性があります。

観点2 観測者の向きの違いによる影響

基準とした(1-3)は、観測者の位置からは見えないものでした。

(1-2)と(1-3)の各要素をそれぞれ比較するため、観点2では、いったん鏡を無くして、観測者の位置や向きという要素に着目します。

観測者が北(鏡側)に回り込む

観測者が文字カードの反対側に回り込むと、(1-3)の見え方になります。

北(鏡側)から見る、ということです。

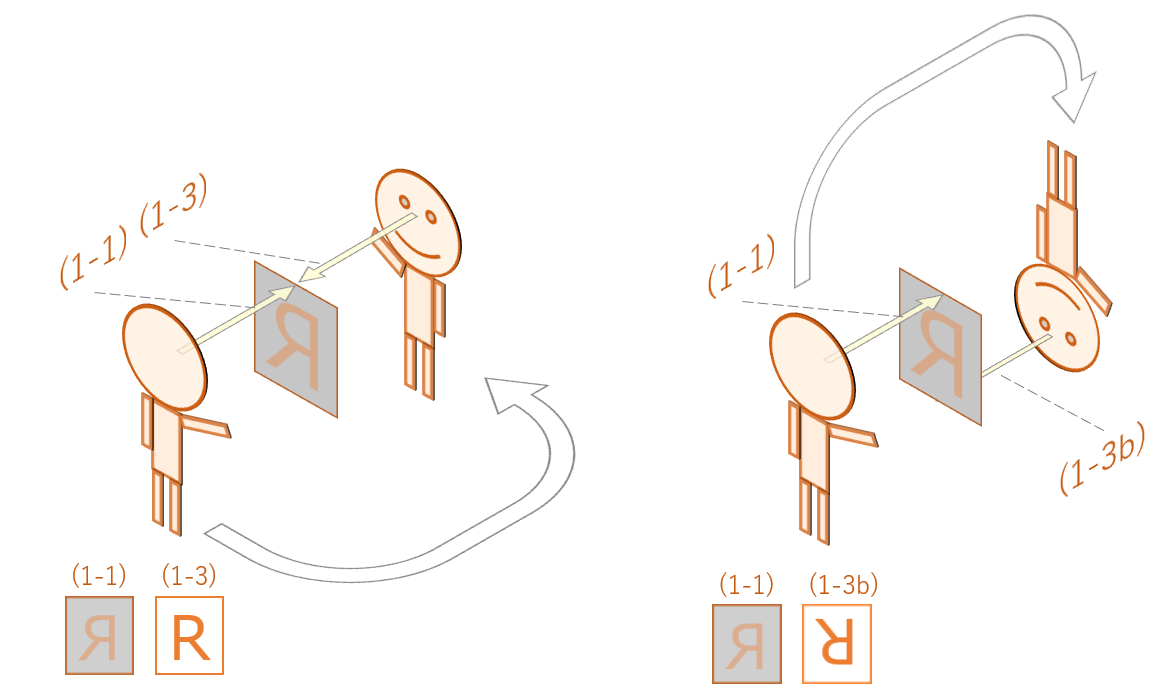
ちなみに、観測者が上(あるいは下)から回り込むと、上下の向きが違う(1-3b)の見え方になります。

本記事では、観点1で決めた、文字として読める”R”の見え方を基準にしますので、観測者の右(あるいは左)から回り込んだ場合の(1-3)のパターンで話を進めます。

回り込みによる左右や上下の入れ替わり

観測者が対象物の裏に回り込むと、観測者の主観において、左右や上下、そして前後が入れ替わるという点にも触れておきます。

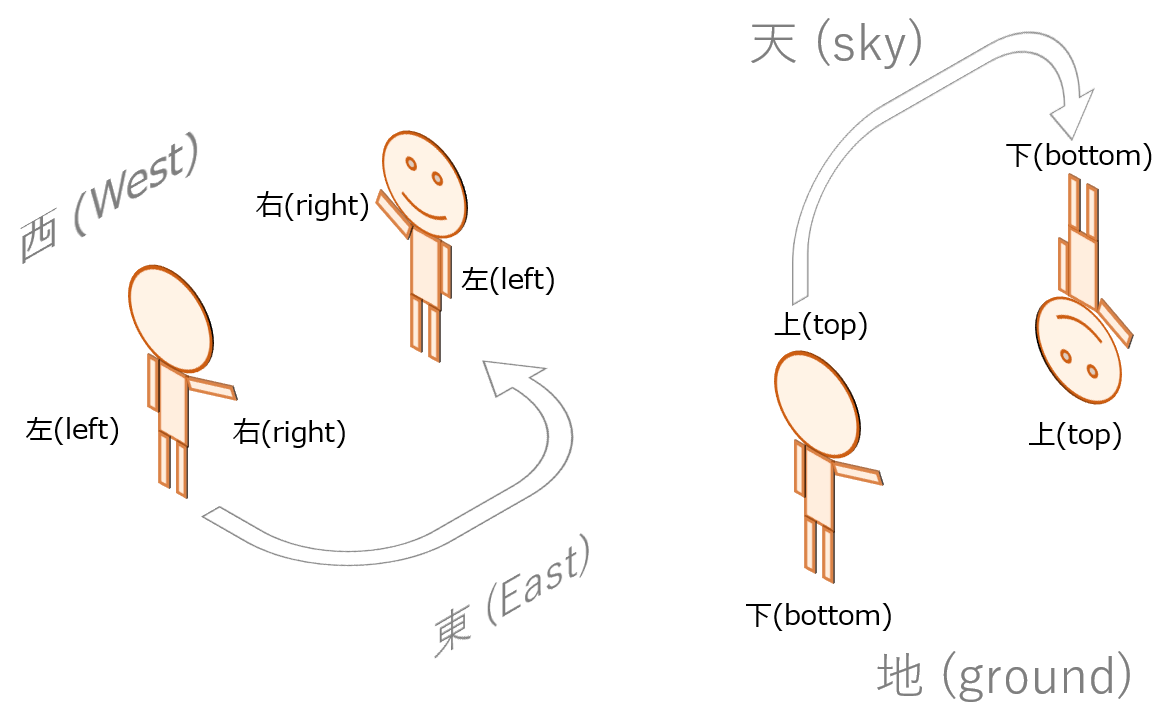
東西は一定ですが、左右は観測者の主観によって変わります。

また、天地も一定ですが、上下は観測者の主観によって変わります。

いずれの場合も、南北に対して前後が入れ替わります(北を向いていた観測者が南を向くため)。

右(あるいは左)から回り込む ＝ 前後と左右が反転する

観点2をまとめます。

観測者が右(あるいは左)から回り込むと、観測者の主観で左右と前後が入れ替わるので、対象物の見え方については、前後反転と左右反転が発生します。

(1-1)と(1-3)を比較すると、表裏が反転し、また文字(裏面からは透けて見える文字)の左右が反転していることが分かります。

観点3 対面する鏡のはたらき

観点3では、観測者の位置や向きは固定したまま、対面する鏡に像を映すと何が起きるのか、という要素に着目します。

鏡により左右反転している訳ではない

文字カードの”R”が、どのように鏡に映っているかを確認します。

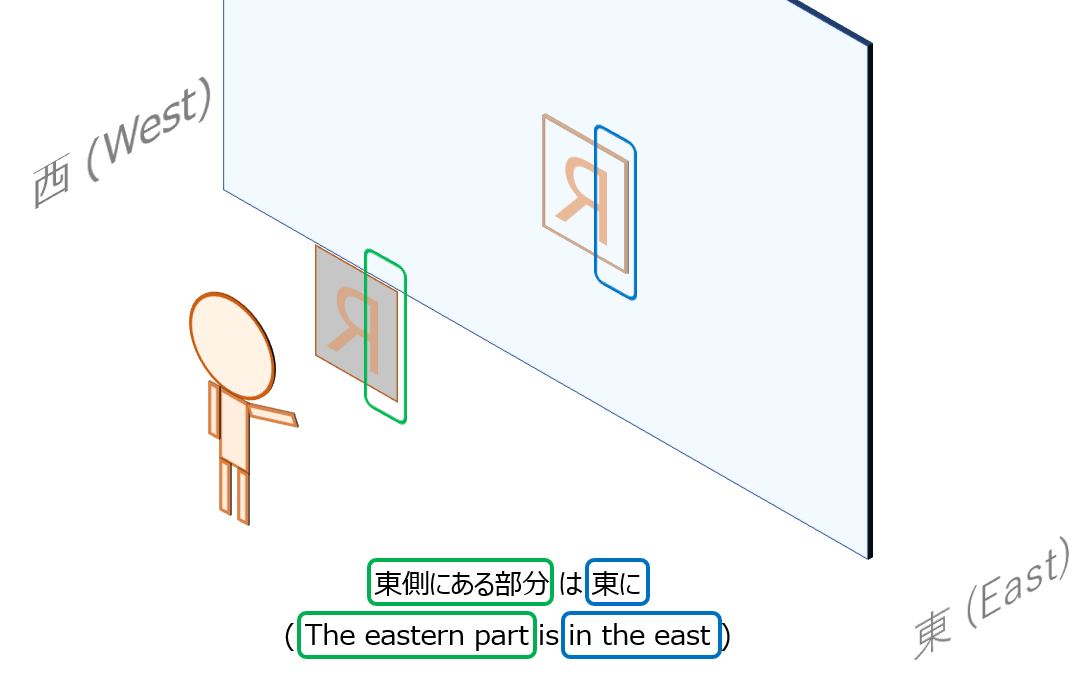
“R”の一部、縦棒に着目すると、東側にあるRの縦棒が、鏡に映ったときも東側に見えます(右左でなく、絶対的な方向である東西を用いて表現しています)。

いま観点3では、鏡の反射に着目するため、観測者の位置や向きを固定しています。他にパラメタが無い以上、鏡に映すこと自体により左右反転はしないということが分かります。

対面する鏡に映す ＝ 前後が反転する

前提として、鏡による反射は、鏡面に対して垂直に反転するということを説明しました。

つまり、観測者が鏡と対面している場合、鏡に映った像は、”前後反転” するということです。

今回、文字カードも観測者も両方、北を向いています。

同じ方向を向いている以上、観測者からは、文字カードの裏しか見えません。

しかし、鏡により反射させることにより、文字カードの表面を、(あえて強調すると)無理やり観測者に見せることができます。つまり前後反転です。

あっちを向いているものをこっちに見せる

観点3をまとめます。

対面する鏡の反射により前後反転する、つまり、ざっくり表現すると、”あっちを向いているものをこっちに見せるはたらき” があると言えます。

これが対面する鏡のはたらきです。

答え

上記の3つの観点から、”どうして、鏡に映ったものは上下には反転せず、左右だけ反転するのだろう？”という疑問を解決していきます。

観点1～3の統合

まず、3つの観点を統合します。

• 観点1 反転しているかどうかを判断するための基準
• 観点2 観測者の向きの違いによる影響
• 観点3 対面する鏡のはたらき

これら3つの観点を図に当てはめると、以下のようになります。

• (1-3)の見え方を基準とし、(1-2)の見え方と比較することとした(観点1)。
• (1-3)と(1-2)の違いは、観測者の向き(観点2)と、鏡に映った像であるかどうか(観点3)。

見え方を構成する各要素の差異が明確に

重要な点は、観点2と観点3を組み合わせることにより、(1-3)と(1-2)を構成する各要素の差異を表現できるということです。

	(1-2)の見え方	(1-3)の見え方 ※基準(観点1)	差異	観点
南北の向き (観測者の視線)	北向き	南向き	あり	観点2
左右の向き	東が右	東が左	あり	観点2
上下の向き	天が上	天が上	なし	観点2
鏡の反射	鏡に映った像	鏡に映った像でない	あり	観点3

差異が明確化され、答えを説明できるようになりました。

ざっくりした答え

まずは、ざっくりした説明です。

• 疑問
  どうして、鏡に映ったものは上下には反転せず、左右だけ反転するのだろう？

• 答え

  • 鏡に映すこと自体により左右反転はしない。
  • しかし、鏡の反射は “あっちを向いているものをこっちに見せるはたらき” があることから、”あっち向きの観測者” が “あっち向きの対象物” を見ることになる。
  • すると、観測者が “あっち向き” のときは、観測者にとっての左右が “こっち向き” の場合とは逆になるため、対象物は左右反転して見える。
    ※ “こっち向きの観測者” が “あっち向きの対象物” を見ると反転しない

本記事の図に対応させると、あっち向き ＝ 北向き、こっち向き ＝ 南向き のことです。

定式化(もどき)による答え

別の答えとして、(1-2) と (1-3) の違いが、観測者の向き (観点2) と、鏡に映った像であるかどうか (観点3) の2点であることに基づき、定式化(もどき)もしてみます。

• (観点2) 観測者の向きが逆であること＝前後反転＋左右反転
  ※今回は観測者が右(あるいは左)から回り込むパターンで話を進めています
• (観点3) 対面する鏡に映すこと＝前後反転

上記より、(1-3) と (1-2) の見え方の差分を求める式は、以下です。

   (1-3) と (1-2) の見え方の差分
= (観点2) 観測者の向きが逆であること + (観点3) 対面する鏡に映すこと
= ( 前後反転 + 左右反転 ) + 前後反転
= ( 前後反転 × 2 ) + 左右反転
= 0 + 左右反転
= 左右反転  

同じ方向に2回反転すると元に戻るので、前後反転×2 は0とみなします。結果、左右反転のみが残ります。

これも、”どうして、鏡に映ったものは上下には反転せず、左右だけ反転するのだろう？” の答えです。

式は任意の組合せに適用可

なお、任意の位置や向きの観測者、対象物、鏡の組合せに対して、上記の式を適用できます。

(1-1) と (1-2) の見え方との比較(観点3のみ)や、あるいは、観測者が上(あるいは下)から回り込むパターン (基準を(1-3b)にして観点2と3) であっても、同様に定式化(もどき)ができるということです。

もう1つの答え　上下反転して見えるケースもあり得る

理解を深めるための別解です。

実は、上記の左右反転についての説明と矛盾せずに、左右反転でなく上下反転して見えるケースもあり得ます。

鏡に映すために、文字カードを裏返したという解釈

ここまでの説明では、前提条件(パラメタ)を1つ省略していました。

もともと文字カードは観測者から読める向きだったと仮定すると、”鏡に映すために文字カードを裏返した” ことになり、その “裏返す方向” が省略していたパラメタです。

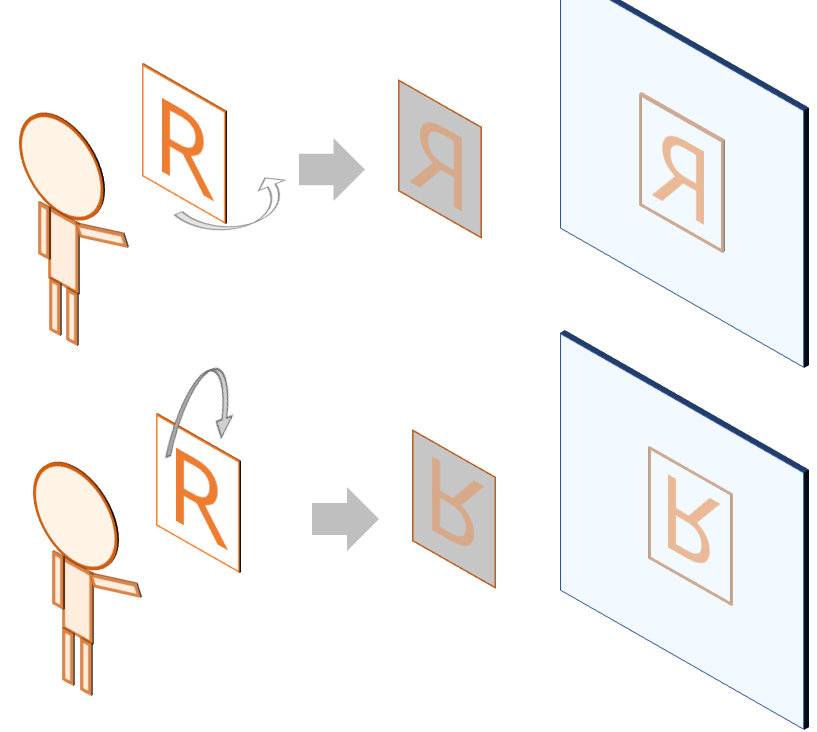
対象物を裏返すと、前後反転と、裏返す方向への反転(左右 or 上下)が発生します。

その裏返す際の方向が左右でなく上下だった場合、この鏡の反転問題は、”どうして上下だけ反転するのだろう？” という疑問に変わってしまう訳です。もちろん上下反転であっても、前述の観点1～3を使って答えにたどり着くことができます。

また、鏡の反転問題を考える方法の１つとして、対象物を裏返す前の見え方を基準として、裏返した後に鏡に映った見え方と比較するといったアプローチもあると言えます。

鏡に映す、相手に見せる ＝ 左右に裏返すケースがほとんど

鏡でなく、向かい合う相手に文字を見せたい場合や、観測者が着ているTシャツに文字がプリントされている場合も同様と言えます。

認知に関連する話かと思いますが、対象物を鏡に映したり、相手に見せるためには、暗黙的に左右に裏返すことが “普通” だと感じるのではないでしょうか。

実際、日常的には、鏡に映したり、相手に見せる際、左右に裏返すことがほとんどでしょう (上下に裏返しても、相手が読めないので慌てて直しますよね)。

私たちは上下逆さまの相手と対面することが基本的に無いので、左右に裏返すことを無意識に “普通” だと感じているのかな、と思います。

観測者の反転

上記は、文字カードを対象物とした場合についての解説でした。

次は、観測者が、鏡に映った自分自身を対象物として見る場合です。

(もちろん物理的には説明を分ける必要性はなく、同じ現象です)

基本的に文字カードを対象物とした場合と同じ

同じ現象なので、仕組みは文字カードの場合と同じです。

ただし、自分自身を対象物とする場合、混乱しやすい場合があるため、いくつか補足します。

観測者の回り込みができない

鏡に映った自分自身を見る場合、文字カードのときのように、観測者の回り込みができません(対象物である自分自身も見えなくなってしまうため)。

そこで、便宜的に、カメラに観測者の代わりをしてもらって、観測者と対象物を分離します。自撮りをするように、自分を映すことにします。

そうすることで、鏡に映った観測者自身と、基準となる見え方(カメラで自撮りした見え方)を比較しやすくなります。

あとは、前述の文字カードと同様に考えれば、答えにたどり着くことができます。

他人をみるときと、鏡に映った自分を見るときの区別が曖昧

以下の図のように、鏡に映った自分の右手と左手の区別に迷う人もいるかもしれません。

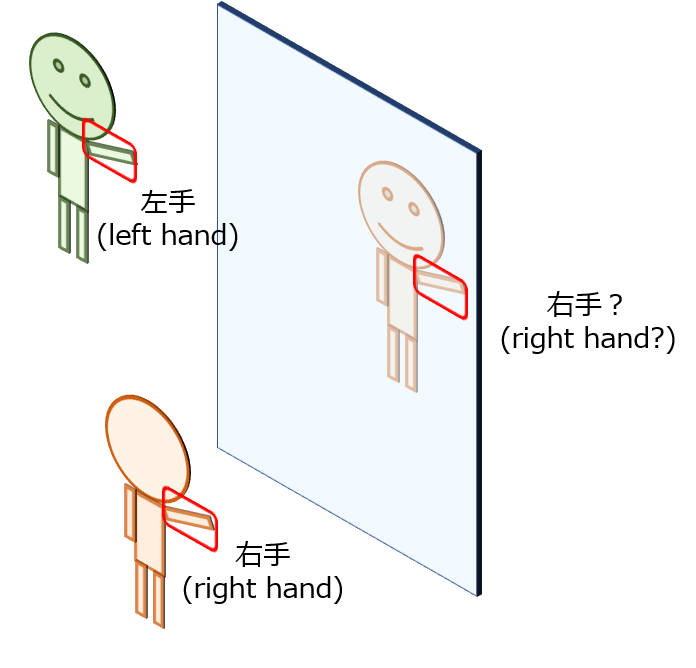
本物の他人と向かい合ったときには左手の位置にある手が、鏡に映った自分の場合、右手(を映したもの)になる訳です。

この “右手か左手か” という区別は、鏡に映った像か、本物の他人かによって、判断を分ける必要性があります。

これは、本記事で扱っている鏡の反転問題とは直接関係ありませんが、混乱しないよう注意すべき点です。

まとめ

本記事では、”鏡に映すと上下でなく左右だけ反転して見えるワケ”についてまとめてみました。

当初の予定より、かなり長い記事になりました。果たしてこんな記事を読む方がいるのか分かりませんが…私は長年の疑問を自分なりに整理したのでスッキリしています。

所感としては、この鏡の反転問題は、論理的なパズルのように楽しむことができました。また、理論は確立しているものの、説明の仕方が色々あるので、ときに説明同士が矛盾するように見えてしまうという特徴があるように思います。

ついでに、記事中で使用した図は、PowerPointのオブジェクトの3D機能で無理やり作成したことも記しておきます。それはそれで面白いのですが、ちゃんと3D描画ソフト的なものの使い方を勉強した方が役に立ちそうです。

余談

自分で実験してみる場合 (自由研究や大人の趣味として)

小学校の自由研究や、大人の趣味的な楽しみとして、実際に試してみるのもオススメです。

以下のようなグッズがあれば、本記事に書かれているような実験ができるでしょう。

まず文字カードです。何か半透明のカード状のものがあれば良いですが、半透明の下敷きでもOKです。

マスキングテープや油性ペンで文字や記号を書けます。

以下は、A5サイズ(148×210mmより少し大きめ)です。A4の半分です。カットして使う場合はケガに気をつけましょう。

鏡は、実験のためだけではなく、家の中で普通に使えるものが良いと思います。

ただ割れるとケガの心配もあるので、ややコンパクトで割れない鏡が良さそうです。実験が終わったら、トイレや玄関等のスペースに置いて身だしなみチェック用の鏡としても使えます。

以下は2枚セットです。

大きな鏡でも実験しやすいと思います。

さらにオプションとしてカメラがあると、”カメラで観測者自身を見る” という視線も試せるので、実験のバリエーションが増えます。

参考

以下のような書籍もあります(参考)。

• 本記事は、Icons8のアイコンを使用しています(Icons by Icons8)。